准备学习大数据的,先按照自己的学习习惯进行知识储备,看看自己能够坚持多长时间吧?
一、高等数学知识
1、常数e,
e=2.71828
努力回想老师的教导,e的用法很多,最初的印象是对数log^e简写成ln^e,然后这个字符在高中、大学数学出现很多,并且在考试中套用各种公式。
2、导数
对导数的记忆就是求导吧,导函数有点印象,多元函数求导好像是大学学的,似乎没学会过(公式背不下来)各种函数的连续性,变化率等都可以用导数描述。
3、梯度
梯度的概念应该在极限的学习中涉猎,记得之前看神经网络学习的材料是,对深度学习的证明就是用梯度的概念进行建模的(详细没记住),不过在这个梯度的应用上用了方向的概念,延伸出向量的知识领域。
4、泰勒-Taylor
泰勒不等式,忘了,反正这帮老数学家给我们留下了宝贵的知识财富,也给我们预留了厚厚的作业.....[2018-10-9]
泰勒级数:

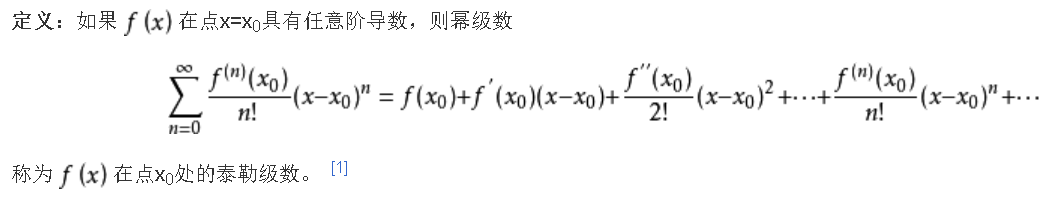

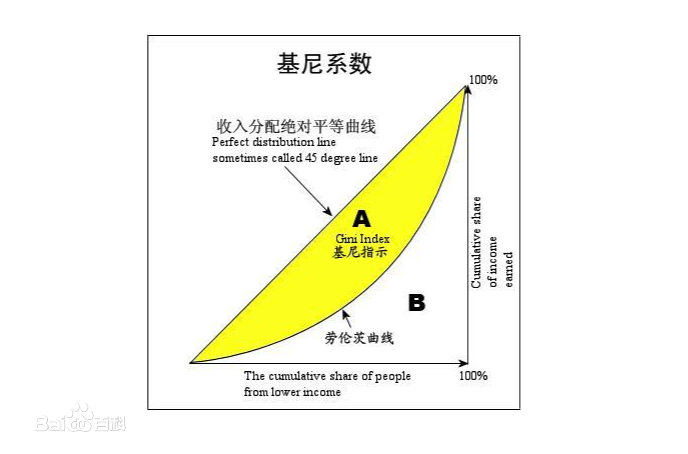
5、gini系数
大家听到最多的就是基尼系数,到底是衡量社会财富分配是否公平,体现社会财富差距和稳定性的一个方式。是计算方式就是A/(A+B),A,B均表示颜色块的面积。具体怎么用还不清楚,初步学习应该跟模型建模相关吧。
6、对数
觉得有必要在回忆下对数的概念。
如果a的x次方等于N(a>0,且a不等于1),那么数x叫做以a为底的N的对数(logarithm),记作x=logaN。其中,a叫做对数的底数,N叫做真数。
称以10为底的对数叫做常用对数(common logarithm),并记为lg
称以无理数e(e=2.71828...)为底的对数称为自然对数(natural logarithm),并记为ln
函数y=logax(a>0&a<>1)叫做对数函数,其中x是自变量。对数函数的定义域是(>0)
基本性质:过定点(1,0),即x=1时,y=0;当0<a<1时,在正无穷上是减函数;当a>1,在正无穷上是增函数。
对数函数运算法则:1、loga(MN)=logaM+logaN
2、loga(M/N)=logaM-logaN
3、logaM^n=nlogaM
4、loga^nM=logaM/n
换底公式

7、梯度下降
梯度下降主要为微分的概念,场景人从山顶下山,但不知道方向,不知道怎么确定到谷底。通过判断该人每步步长的下降高度。数学公式的求证,应用都在理想场景,所以在学习过程中千万纠结公式字面和实际情况。理解透了就可以。
尽管梯度下降为机器学习的关键,本次不强求自己吃透。
8、牛顿法:准确说应该为牛顿迭代法,近似求解方程的方法。使用函数f(x)的泰勒级数的前面几项来寻解方程的f(y)=0的根。
学习参考链接:https://www.zhihu.com/question/20690553 ;https://www.cnblogs.com/shixiangwan/p/7532830.html
二、概率论
微积分与逼近论;极限,微分,积分基本概念;利用逼近的思想理解微分,利用积分的方式理解概率;概率论基础。
感觉学的还行,但是让我用一口气讲出来,就比较难了,本次先不纠结这些内容。

截图是从一个培训课程文件截图,如果涉及到其他问题,烦请联系我。